Research

Quantum annealing is one of the leading paradigms in quantum computing. Annealing consists of driving a system to the ground state of a Hamiltonian that encodes the solution to a problem of interest. Finding such a ground state is tantamount to computation. In adiabatic quantum computing, the target ground state is reached by driving the system sufficiently slowly. However, this can be overly conservative, and general protocols can sometimes compute a lot faster than adiabatic ones. Then, what is the minimum time needed to compute?

In [PRL 2023] we derived inequalities that constrain the minimum computation times of any annealing protocol. The inequalities are saturable, that is, they accurately reflect the minimum computation times in some cases. These results can be use to benchmark analog quantum algorithms.

Speed limits are uncertainty relations that bound the rate of change of a physical system. We have derived bounds on the speed with which any physical quantity evolves in a classical system [Nat Phys 2020], and we have constructed a framework that generalizes these bounds to classical or quantum systems with arbitrary dynamics [PRX 2022]. These speed limits bound how fast entropy or heat can be transferred from a system.

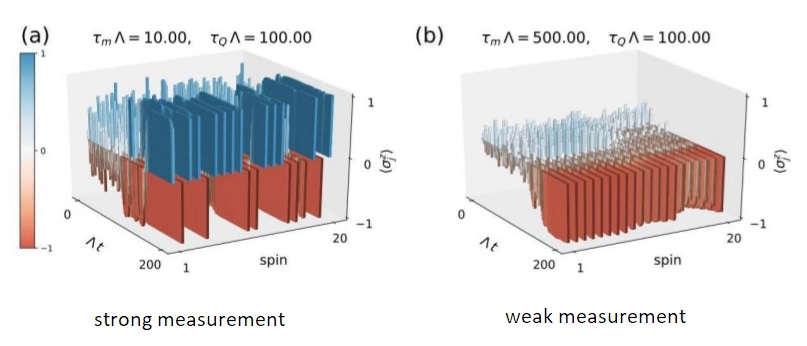
Measurements have a very special role in quantum theory, affecting the subsequent evolution of a state. I have focused on the effects that monitoring a quantum system has on its dynamics.

In [PRL 2019] we studied the measurement back-action on monitored quantum systems as mechanism driving the process of Symmetry Breaking, relevant to a wide range of physical phenomena. The properties of the symmetry broken state is in such case drastically dependent on the nature of the quantum measurements performed. This raises the interesting prospect of exploiting measurement back-action [PRL 2018] in many-body systems.

The amount of work W stored in a battery is not its only important figure of merit to characterize it – it is also important to be able to extract or store such work rapidly enough, and to have a handle on the fluctuations of W.

In [PRL 2020] we studied the connection between the charging power of a quantum battery and the fluctuations of the work stored in the battery. We proved that in order to have a non-zero rate of change of the extractable work, the work fluctuations must be non-zero.  This manifests itself in terms of an uncertainty relationship that fundamentally bounds the speed of the charging process of any quantum system.

Sufficiently large isolated quantum systems equilibrate under very general conditions. However, there exist observables that do so in extremely long times (longer than the age of the universe even for quite small systems!) [PRE 2014]. It is thus essential to restrict to physically meaningful observables in order to prove fast equilibration.

In [PRX 2017] we found conditions on the observable, initial state, and Hamiltonian of a system which ensure equilibration occurs within short time scales. These bounds are tight, and significantly simpler to calculate than solving the exact dynamics of the system.

These techniques can be used, for instance, to study the dynamics of correlation functions in many-body quantum systems. There, we found estimates on their timescales in regimes otherwise inaccessible with numerical or theoretical methods [PRL 2020].

In general, quantum states cannot be interpreted as classical probability distributions. In particular, given a coherent superposition of two states, one cannot think of the system as being in either of those states, with a certain probability for each. In unitary quantum mechanics these superposition states always remain as such, a fact that is at the root of the difficulty in defining the occurrence of quantum events.

However, it is only with access to an ideal clock that one would be able to perceive the underlying unitary evolution of a quantum system in an experiment. A combination of quantum mechanical (QM) and general relativity (GR) arguments indicate that such perfect clocks are unlikely to exist.

We showed [PRA 2019] that if fundamental time uncertainties exist, then situations naturally arise in which no measurement allows to verify that a system is in a quantum superposition. That is, from the point of view of physically observable predictions, in such situations the system behaves exactly as if it were in a classically interpretable state. We built on this idea to develop the Montevideo Interpretation of Quantum Mechanics, a realist view of how events and measurements happen in a quantum world.